Recentemente, foi incluído grande volume de material de Geometria do período védico da Índia no artigo de História da Geometria da Wikipédia em inglês. Isso levou-me a preparar essa tradução, complementar ao volume anterior de História da Geometria.
O período védico indiana teve uma tradição de geometria, expresso sobretudo na construção de altares elaborados. Textos indianos iniciais (1º milênio a.C.) sobre este tema incluem o Satapatha Brahmana e o Śulba Sūtras.[4][5][6]
Manuscrito Rigveda em Devanagari.
De acordo com (Hayashi 2005, p. 363), os Śulba Sūtras contém "a expressão verbal existente mais antiga do Teorema de Pitágoras no mundo, embora já tivesse sido conhecido para os antigos babilônicos."
“A corda diagonal (akṣṇayā-rajju) de um (retângulo) oblongo produz tanto como as (cordas) do flanco (pārśvamāni) e a horizontal (tiryaṇmānī) produzem separadamente."[7]
Eles contêm listas de trios pitagóricos,[8] que são casos particulares de equações diofantinas.[9] Também contêm afirmações (que com retrospectiva que sabemos ser aproximado) sobre a quadratura do círculo e "circulatura do quadrado".[10]
O Baudhayana Śulba Sūtra, o mais conhecido e antigo Śulba Sūtra (datado dos séculos VIII ou VII a.C.) contém exemplos de trios pitagóricos simples, tais como: (3, 4, 5), (5, 12, 13), (8 , 15, 17), (7, 24, 25), e (12, 35, 37),[11] bem como o estabelecimento do teorema de Pitágoras para os lados de um quadrado: "a corda que é esticada entre os diagonal de um quadrado produz uma área duas vezes o tamanho do quadrado original "[11] Também contém a instrução geral do teorema de Pitágoras (para os lados de um rectângulo): "A corda esticada ao longo do comprimento da diagonal de um retângulo faz uma área que os lados verticais e horizontais fazem em conjunto."[11]
De acordo com o matemático S.G. Dani, a tábua cuneiforme babilônica Plimpton 322, escrita em 1850 a.C.[12] "contém quinze trios pitagóricos com valores bastante grandes, incluindo (13500, 12709, 18541), que é um trio primitivo,[13], o que indica, em particular, que havia sofisticada compreensão sobre o tema" na Mesopotâmia em 1850 a.C.. "Uma vez que estas tábuas são anteriores ao período Śulba Sūtras por vários séculos, tendo em conta o aspecto contextual de algumas dos trios, é razoável esperar que compreensão semelhante teria ocorrido na Índia."[14] Dani continua dizendo:
"Como o principal objetivo do Śulba Sūtras foi descrever as construções de altares e os princípios geométricos envolvidos neles, objeto de trios pitagóricos, mesmo se isso tivesse sido bem entendido podendo ainda não ter sido apresentado no Śulba Sūtras. A ocorrência dos triplos no Śulba Sūtras é comparável à matemática que se pode encontrar em um livro introdutório sobre arquitetura ou de outra área aplicada semelhante, e não correspondem diretamente ao conhecimento geral sobre o tema nesse momento. uma vez que, infelizmente, não há outras fontes contemporâneas que tenham sido encontrados e isso pode nunca ser possível de ser resolvido como problema de forma satisfatória."[14]
Ao todo, três Śulba Sūtras foram compostos. Os dois restantes, o Manava Śulba Sūtra composto por Manava (fl. 750-650 aC) e o Apastamba Śulba Sūtra, composto por Apastamba (c. 600 a.C.), continha resultados semelhantes ao Baudhayana Śulba Sūtra.
Nota do tradutor:
Referência a ser acrescentada aqui:
The Thirteen Books of Euclib's Elements. CUP Archive, 1926. pg 360 - books.google.com.br
Referências
4. A. Seidenberg, 1978. The origin of mathematics. Archive for the history of Exact Sciences, vol 18.
4. A. Seidenberg, 1978. The origin of mathematics. Archive for the history of Exact Sciences, vol 18.
5. (Staal 1999)
6. A maioria dos problemas matemáticos considerados no Śulba Sūtras concentram-se em "uma única exigência teológica", que é a da construção de altares de fogo que tenham diferentes formas, mas ocupem a mesma área. Os altares deviam obrigatoriamente ser construídos de cinco camadas de tijolos queimados, ainda com a condição de que cada camada consistia em 200 tijolos e que não há duas camadas adjacentes que tenham concordância congruentes de tijolos. (Hayashi 2003, p. 118)
7. (Hayashi 2005, p. 363)
8. Trios pitagóricos são trios de inteiros 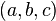 com a propriedade:
com a propriedade: 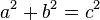 . Então,
. Então, 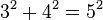 ,
,  ,
, 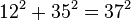 , etc.
, etc.
9. (Cooke 2005, p. 198): "O conteúdo aritmético do Śulva Sūtras consiste de regras para encontrar trios pitagóricos tais como (3, 4, 5), (5, 12, 13), (8, 15, 17) e (12, 35, 37). Não é certo qual utilização prática tinham essas regras aritméticas. A melhor conjectura é que eles eram parte de um ritual religioso. Uma casa Hindu era obrigada a ter três fogueiras que queimavam em três altares diferentes. Os três altares eram para ser de formas diferentes, mas todos os três eram para ter a mesma área. Estas condições originaram a alguns problemas "Diofantinos", caso particular dos quais é a geração de trios pitagóricos, de modo a obter um número inteiro quadrado igual à soma de outros dois."
10. (Cooke 2005, pp. 199–200): "A exigência de três altares de áreas iguais, mas diferentes formas explicaria o interesse na transformação de áreas. Entre outros problemas de transformações de áreas os Hindus consideravam, em particular, o problema da quadratura do círculo. O Bodhayana Sutra declara o problema inverso de construção de um círculo igual a um determinado quadrado. A construção seguinte aproximada é dada como a solução .... este resultado é apenas aproximado. Os autores, no entanto, não fazem distinção entre os dois resultados. Em termos que podemos apreciar, esta construção dá um valor para π de 18 (3 − 2√2), o que é aproximadamente 3.088."
11. (Joseph 2000, p. 229)
13. Três inteiros positivos 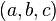 formam um trio pitagórico primitivo se
formam um trio pitagórico primitivo se  e se o mais alto fator comum de
e se o mais alto fator comum de 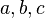 é 1 (são “primos entre si”). No exemplo particular do documento Plimpton 322, isso significa que
é 1 (são “primos entre si”). No exemplo particular do documento Plimpton 322, isso significa que  e que os três números não têm quaisquer fatores comuns. No entanto, alguns estudiosos têm contestado a interpretação pitagoreana desta tábula; ver Plimpton 322 para detalhes.
e que os três números não têm quaisquer fatores comuns. No entanto, alguns estudiosos têm contestado a interpretação pitagoreana desta tábula; ver Plimpton 322 para detalhes.
14. (Dani 2003)
Leituras recomendadas
Jean Michel Delire; Quadratures, circulature and the approximation of √2 in the Indian Śulba-sútras; Centaurus, Volume 47, Issue 1, pages 60–71, February 2005
DOI: 10.1111/j.1600-0498.2005.00018.x - onlinelibrary.wiley.com
Kim Plofker; Mathematics in India; Princeton University Press, 2008. - books.google.com.br
Bibhutibhusan Datta; Origin and History of the Hindu names for Geometry; Quellen und Studien zur Geschichte der Mathematik, 1930, pp 113-119. - link.springer.com
Raghunātha Purushottama Kulakarṇī; Geometry according to Śulba sūtra; Tilak Mahārāśtra Vidyāpīṭha, Vaidika Saṁśodhana Maṇḍala, 1983. -




Nenhum comentário:
Postar um comentário