quinta-feira, 13 de agosto de 2015

Matemática indiana - 4



Quarta parte da tradução de en.wikipedia.org - Indian mathematics


Período clássico (400–1600 d.C.)
Este período é muitas vezes conhecido como a “idade de ouro” da matemática indiana. Este período viu matemáticos como Aryabhata, Varahamihira, Brahmagupta, Bhaskara I, Mahavira, Bhaskara II, Madhava de Sangamagrama e Nilakantha Somayaji dar mais ampla e clara forma a muitos ramos da matemática. Suas contribuições se espalhariam pela Ásia, o Oriente Médio, e, eventualmente, para a Europa. Ao contrário da matemática védica, seus trabalhos incluíram tanto contribuições astronômicos como matemáticas. Na verdade, a matemática desse período foi incluído na "ciência astral” (jyotiḥśāstra) e consistiu em três sub-disciplinas: Ciências matemáticas (gaṇita ou tantra), horóscopo astrológico (horā ou jātaka) e adivinhação (saṃhitā).[46] Essa divisão tripartite é vista na compilação de Varahamihira do século VI — Pancasiddhantika [61] (literalmente panca, "cinco", siddhānta, "conclusão de deliberação", ou mais propriamente, “cinco princípios”, datado de 575 d.C.) — de cinco obras anteriores, Surya Siddhanta, Romaka Siddhanta, Paulisa Siddhanta, Vasishtha Siddhanta e Paitamaha Siddhanta, que eram adaptações de obras ainda anteriores da astronomia da Mesopotâmia, gregos, egípcios, romanos e indianos. Como explicado anteriormente, os textos principais foram compostos em versos em sânscrito, e foram seguidos por comentários em prosa.[46]   


Este fac-símile do Pancasiddhantika, mostra graficamente como eclipses devem ser calculados. Este texto prenuncia o que astrônomos ocidentais propuseram quase um milênio depois.  - www.hindubooks.org


Séculos quinto e sexto


Surya Siddhanta
Apesar de sua autoria ser desconhecida, o Surya Siddhanta (c. 400) contém as raízes da trigonometria moderna. Devido a conter muitas palavras de origem estrangeira, alguns autores consideram que ele foi escrito sob a influência da Mesopotâmia e Grécia.[62]

Nota do tradutor: Referências de Surya Siddhanta como contendo raízes da trigonometria:

Zaheer Baber; The Science of Empire: Scientific Knowledge, Civilization, and Colonial Rule in India; SUNY Press, 1996. pg 31.

Dick Teresi; Lost Discoveries: The Ancient Roots of Modern Science - from the Babylonians to the Maya; Simon and Schuster, 2010. pg 131.
G. H. A. Cole; The Inverted Bowl: Introductory Accounts of the Universe and Its Life; World Scientific, 2010. pg 299.


Este texto antigo usa as seguintes funções trigonométricas pela primeira vez:
  • Seno (Jya).
  • Cosseno (Kojya).
  • Arco seno (Otkram jya).
Também contém os primeiros usos de:
  • Tangente.
  • Secante.
Mais tarde matemáticos indianos como Aryabhata fizeram referências a este texto, enquanto traduções árabes e latino posteriores foram muito influentes na Europa e no Oriente Médio.


Calendário Chhedi
O calendário Chhedi (594) contém um uso precoce do moderno sistema de posição-valor do sistema numérico hindu-arábico agora usado universalmente (ver também algarismos hindu-arábicos).


Aryabhata I
Aryabhata (476-550) escreveu o Aryabhatiya. Ele descreveu os princípios fundamentais importantes da matemática em 332 shlokas. O tratado continha:
  • Equações quadráticas
  • Trigonometria
  • O valor de π, correto até a 4a casa decimal.
Aryabhata também escreveu o Arya Siddhanta, o qual se encontra atualmente perdido. A scontribuições de Aryabhata incluem:
Trigonometria:
  • Introduziu as funções trigonométricas.
  • Definiu o seno (jya) como moderna relação entre a metade de um ângulo e metade de uma corda.
  • Definiu o cosseno (kojya).
  • Definiu o seno verso (utkrama-jya).
  • Definiu o arco seno (seno inverso, otkram jya).
  • Gave methods of calculating their approximate numerical values.
  • Contém as primeiras tabelas de valores de seno, cosseno e seno verso, em intervalos de 3,75° de 0 ° a 90 °, com 4 casas decimais de precisão.
  • Contém a fórmula trigonométrica sen(n + 1)x − sen nx = sen nx − sin(n − 1)x − (1/225)sen nx.
  • Trigonometria esférica.
Aritmética:
  • Frações contínuas.
Álgebra:
  • Soluções de equações quadráticas simultâneas.
  • Soluções de números inteiros de equações lineares por um método equivalente ao método moderno.
  • Solução geral da equação linear indeterminada.
Astronomia matemática:
  • Cálculos precisos para constantes astronômicas, como:
    • Eclipse solar.
    • Eclipse lunar.
    • A fórmula para a soma dos cubos, o que foi um passo importante no desenvolvimento de cálculo integral.[63]   


Varāhamihira

Varāhamihira (505–587) produziu o Pancha Siddhanta (Os Cinco Cânones Astronômicos). Fez importantes contribuições para a trigonometria, incluindo tabelas de seno e cosseno com precisão até 4 casas decimais e as seguintes fórmulas relacionando as funções de seno e cosseno:
  • \sin^2(x) + \cos^2(x) = 1
  • \sin(x)=\cos\left(\frac{\pi}{2}-x\right)
  • \frac{1-\cos(2x)}{2}=\sin^2(x)


Séculos sétimo e oitavo


O teorema de Brahmagupta estabelece que AF = FD.
No século VII, dois campos separados, aritmética (que incluiu medição) e álgebra, começaram a surgir na matemática indiana. Os dois campos mais tarde seriam chamados pāṭī-gaṇita (literalmente "matemática de algoritmos") e bīja-gaṇita (lit. "matemática de sementes", com "sementes" tendo o sentido de sementes de plantas - representando incógnitas com o potencial de gerar, neste caso, as soluções de equações).[64] Brahmagupta, em seu trabalho astronômico Brāhma Sphuṭa Siddhānta (628 d.C.), incluiu dois capítulos (12 e 18) dedicados a estes campos. O capítulo 12, que contém 66 versos em sânscrito, foi dividido em duas seções: "operações básicas" (incluindo raízes cúbicas, frações, razão e proporção e permutações) e "matemática prática" (incluindo misturas, séries matemáticas, figuras planas, empilhamentos de tijolos, serragem de madeira e grãos).[65] Neste último ponto, ele declarou seu famoso teorema sobre as diagonais de um quadrilátero cíclico:[65]    


Teorema de Brahmagupta: Se um quadrilátero cíclico tem diagonais que são perpendiculares uma a outra, então a linha perpendicular traçada a partir do ponto de interseção das diagonais para qualquer lado do quadrilátero sempre corta o lado oposto.
O capítulo 12 também inclui uma fórmula para a área de um quadrilátero cíclico (uma generalização da fórmula de Heron), bem como uma descrição completa dos triângulos racionais (isto é, os triângulos com lados racionais e áreas racionais).
Fórmula de Brahmagupta: A área, A, de um quadrilátero cíclico com lados de comprimentos a, b, c, d, respectivamente, é dada por
A = \sqrt{(s-a)(s-b)(s-c)(s-d)}
onde s, o semiperímetro, é dado por: s=\frac{a+b+c+d}{2}.
Teorema de Brahmagupta sobre triângulos racionais: Um triângulo com lados racionais 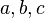a, b, c e área racional é da forma:
a = \frac{u^2}{v}+v, \ \ b=\frac{u^2}{w}+w, \ \ c=\frac{u^2}{v}+\frac{u^2}{w} - (v+w)
para números racionais 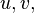u, v, e w .[66]
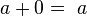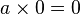O capítulo 18 contém 103 versos em sânscrito os quais iniciam com regras para operações aritméticas envolvendo zero e números negativos e é considerada o primeiro tratamento sistemático do assunto.[65] As regras (que incluíam a + 0 = \ a e a \times 0 = 0 ) estavam todas corretas, com uma exceção: 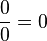\frac{0}{0} = 0 .[65] Mais adiante, no capítulo, ele apresenta a primeira solução explícita (embora ainda não completamente geral) da equação quadrática:
\ ax^2+bx=c
“Para o número absoluto multiplicado por quatro vezes o [coeficiente do] quadrado, adicionar o quadrado do [coeficiente do] termo médio; a raiz quadrada da mesma, menos o [coeficiente do] termo médio, sendo dividido por duas vezes o [do coeficiente] quadrado é o valor.”



Isto é equivalente a:
x = \frac{\sqrt{4ac+b^2}-b}{2a}

Também no capítulo 18, Brahmagupta foi capaz de fazer progressos na busca de soluções (inteiras) da equação de Pell, [67]
\ x^2-Ny^2=1,
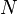onde N é um inteiro não quadrado. Ele fez isso por descobrir a seguinte identidade:[68]

Identidade de Brahmagupta:
\ (x^2-Ny^2)(x'^2-Ny'^2) = (xx'+Nyy')^2 - N(xy'+x'y)^2 a qual é uma generalização de uma identidade mais primordial de Diofante.[68] Brahmagupta usou essa identidade para provar o seguinte lema:[68]
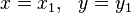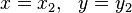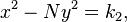Lema (Brahmagupta): Se x=x_1,\ \ y=y_1 \ \ é uma solução de \ \ x^2 - Ny^2 = k_1, e, x=x_2, \ \ y=y_2 \ \ é uma solução de \ \ x^2 - Ny^2 = k_2, , então:
x=x_1x_2+Ny_1y_2,\ \ y=x_1y_2+x_2y_1 \ \ é uma solução de \ x^2-Ny^2=k_1k_2
Ele então usou esse lema tanto para gerar um número infinito de soluções (inteiras) da equação de Pell, dada uma solução, e declarar o seguinte teorema:
Teorema (Brahmagupta): Se a equação 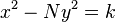\ x^2 - Ny^2 =k tem uma solução inteira para qualquer um de \ k=\pm 4, \pm 2, -1 entãoa equação de Pell:
\ x^2 -Ny^2 = 1

também tem uma solução inteira.[69]     
Brahmagupta não chegou a provar o teorema, mas trabalhou com exemplos usando seu método. O primeiro exemplo apresentado foi:[68]
Exemplo (Brahmagupta): Encontre inteiros 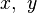\ x,\ y\ tais que:
\ x^2 - 92y^2=1

Em seu comentário, Brahmagupta adicionou, "uma pessoa solucionando este problema dentro de um ano é um matemático."[68] A solução que ele forneceu foi:
\ x=1151, \ y=120

Bhaskara I
Bhaskara I (c. 600–680) expandiu o trabalho de Aryabhata em seus livros intitulados Mahabhaskariya, Aryabhatiya-bhashya e Laghu-bhaskariya. Ele produziu:
Soluções de equações indeterminadas.
Uma aproximação racional da função seno.
Uma fórmula para o cálculo do seno de um ângulo agudo sem o uso de uma tabela, correta a duas casas decimais.


Séculos nono a duodécimo
Virasena
Virasena (século VIII) foi um matemático Jain na corte de Rashtrakuta, rei Amoghavarsha de Manyakheta, Karnataka. Ele escreveu o Dhavala, um comentário sobre matemática Jain, o qual:
  • Lidou com o conceito de ardhaccheda, o número de vezes que um número poderia ser dividido à metade; efetivamente logaritmos de base 2, e enumera várias regras que envolvem esta operação.[70][71]   
  • Usou pela primeira vez logaritmos de base 3 (trakacheda) e base 4 (caturthacheda).
Virasena também apresentou:
  • A derivação do volume do frustum (tronco de bases paralelas) por uma espécie de procedimento infinito.
Pensa-se que a maior parte do material de matemática no Dhavala pode ser atribuido a escritores anteriores, especialmente Kundakunda, Shamakunda, Tumbulura, Samantabhadra e Bappadeva e são datados como tendo sido escritos entre 200 e 600 d.C.[71]     
Mahavira
Mahavira Acharya (c. 800–870) de Karnataka, o último dos notáveis matemáticos Jain, viveu no século IX e foi patrocinado por Rashtrakuta, rei Amoghavarsha. Escreveu um livro chamado Ganit Saar Sangraha em matemática numérica, e também escreveu tratados sobre uma ampla gama de temas matemáticos. Estes incluem a matemática de:
  • Zero
  • Quadrados
  • Cubos
  • Raízes quadradas, raízes cúbicas, e as séries estendendo-se além dessas
  • Geometria plana
  • Geometria sólida
  • Problemas relacionados com a formação de sombras
  • Fórmulas derivadas para calcular a área de uma elipse e quadrilátero dentro de um círculo.
Mahavira também:
  • Afirmou que a raiz quadrada de um número negativo não existia.
  • Apresentou a soma de uma série cujos termos são quadrados de uma progressão aritmética, e deu regras empíricas para a área e o perímetro de uma elipse.
  • Resolveu equações cúbicas.
  • Resolveu equações quárticas.
  • Resolveu algumas quínticas e polinômios de ordens mais altas.
  • Apresentou as soluções gerais das equações polinomiais de ordem mais alta:
    • \ ax^n = q
    • a \frac{x^n - 1}{x - 1} = p
  • Resolveu equações quadráticas indeterminadas.
  • Resolveu equações cúbicas indeterminadas.
  • Resolveu equações indeterminadas de ordem mais alta.
Shridhara
Shridhara (c. 870–930), que viveu em Bengala, escreveu os livros intitulados Nav Shatika, Tri Shatika e Pati Ganita. Ele apresentou:
  • Uma eficiente regra para encontrar-se o volume de uma esfera.
  • A fórmula para resolver-se equações quadráticas.
O Pati Ganita é um trabalho sobre aritmética e medida. Trata-se de várias operações, incluindo:
  • Operações elementares
  • Extração de raízes quadradas e cúbicas.
  • Frações.
  • Oito regras são apresentadas para operações envolvendo zero.
  • Métodos de somatório de diferentes séries aritméticas e geométricas, que viriam a se tornar referências padrão em trabalhos posteriores.
Manjula
As equações diferenciais de Aryabhata foram elaboradas no século X por Manjula (também Munjala), que apresentou a seguinte expressão [72]  
\ \sin w' - \sin w
que pode ser expressa aproximadamente como

\ (w' - w)\cos w
Ele entendeu o conceito de diferenciação depois de resolver a equação diferencial que resultou substituindo esta expressão na equação diferencial de Aryabhata.[72]    
Aryabhata II
Aryabhata II (c. 920–1000) escreveu um comentário sobre Shridhara, e um tratado astronômico, Maha-Siddhanta. O Maha-Siddhanta tem 18 capítulos, e discute:
  • Matemática numérica (Ank Ganit).
  • Álgebra.
  • Soluções de equações indeterminadas (kuttaka).
Shripati
Shripati Mishra (1019–1066) escreveu os livros Siddhanta Shekhara, um grande trabalho sobre astronomia em 19 capítulos, e Ganit Tilaka, um tratado aritmético incompleto em 125 versos baseado em um trabalho de Shridhara. Trabalhou principalmente em:
  • Permutações e combinações.
  • Solução geral da equação linear simultânea indeterminada.
Também foi autor de Dhikotidakarana, um trabalho de vinte versos sobre:
  • Eclipse solar.
  • Eclipse lunar.
O Dhruvamanasa é um trabalho de 105 versos sobre:
  • Cálculo das longitudes planetárias.
  • Eclipses.
  • Trânsitos planetários.


Nemichandra Siddhanta Chakravati
Nemichandra Siddhanta Chakravati (c. 1100) foi autor de um tratado matemático intitulado Gome-mat Saar.
Bhaskara II
Bhāskara II (1114–1185) foi um matemático-astrônomo que escreveu uma série de tratados importantes, a saber, o Siddhanta Shiromani, Lilavati, Bijaganita, Gola Addhaya, Griha Ganitam e Karan Kautoohal. Um número significativo de suas contribuições foram posteriormente transmitidas para o Oriente Médio e Europa. Suas contribuições incluem:
Aritmética:
  • Cálculo de juros
  • Progressões aritméticas e geométricas
  • Geometria plana
  • Geometria sólida
  • A sombra do gnômon
  • Soluções de combinações
  • Apresentou uma demonstração para a divisão por zero sendo a infinidade.
Álgebra:
  • O reconhecimento de um número positivo como tendo duas raízes quadradas.
  • Raízes n-ésimas.
  • As operações com produtos de várias incógnitas.
  • As soluções de:
    • Equações quadráticas.
    • Equações cúbicas.
    • Equações quárticas.
    • Equações com mais de uma incógnita.
    • Equações quadráticas com mais de uma incógnita.
    • A forma geral da equação de Pell usando o método chakravala.
    • A equação quadrática indeterminada geral  usando o método chakravala.
    • Equações cúbicas indeterminadas.
    • Equações quárticas indeterminadas.
    • Equações polinomiais de ordem mais alta indeterminadas.
Geometria:
  • Apresentou uma demonstração do teorema de Pitágoras.
Cálculo:
  • Concebeu o cálculo diferencial.
  • Descobriu a derivada.
  • Descobriu o coeficiente diferencial.
  • Desenvolveu a diferenciação.
  • Estabeleceu o teorema de Rolle, um caso especial do teorema do valor médio (um dos teoremas mais importantes em cálculo e análise).
  • Derivou a diferencial da função seno.
  • Calculou π, correto até cinco casas decimais.
  • Calculou o comprimento da revolução da Terra ao redor do Sol até 9 casas decimais.
Trigonometria:
  • Desenolvimentos de trigonometroa esférica.
  • As fórmulas trigonométricas:
    • \ \sin(a+b)=\sin(a) \cos(b) + \sin(b) \cos(a)
    • \ \sin(a-b)=\sin(a) \cos(b) - \sin(b) \cos(a)



Notas, Obras Fonte em Sânscrito e Referências ainda em tradução podem ser encontradas provisoriamente em: Google Drive - Matematica indiana - 7 e Matematica indiana - 8



Leituras recomendadas

Miscellaneous Essays, Volume 2; Henry Thomas Colebrooke, Wm. H. Allen, 1837 -

Asiatick Researches; Or, Transactions, Volume 2; Asiatic Society (Calcutta, India), 1807 -

Asiatic Researches; Or, Transactions of the Society, Instituted in Bengal,: For Inquiring Into the History and Antiquities, the Arts, Sciences, and Literature, of Asia. ... Printed Verbatim from the Calcutta Edition..; Asiatic Society of Bengal; J. Sewell; Vernor and Hood; J. Cuthell; J. Walker; R. Lea; Lackington, Allen, and Company; Otridge and son; R. Faulder; and J. Scatcherd., 1808 - books.google.com.br
Ravi Agarwal, Syamal Sen; Creators of Mathematical and Computational Sciences; Springer, 2014 - books.google.com.br
Asiatick Researches, Or, Transactions of the Society Instituted in Bengal, for Inquiring Into the History and Antiquities, the Arts, Sciences, and Literature, of Asia, Volume 2; J. Swan and Company, 1801 - books.google.com.br

Postado por às

Nenhum comentário:

Postar um comentário

Assinar: Postar comentários (Atom)